Scratchでよく使われる便利なコードの使用例です。今回は「跳ね返りの法則」です。これを参考にいろいろと試してください。
スプライトの跳ね返り
いろんなゲームなどを作るときには画面を移動しているスプライトを跳ね返らせるプログラムはよく書きます。
「端に着いたら、跳ね返る」ブロックは、画面の端に着いたら跳ね返る動作をブロック1つで実行してくれるので、とても便利なためよく使われているかと思います。
このブロックは文字通り端に着いたら跳ね返りますが、他のスプライトに当たっても跳ね返りません。
どうすれば他のスプライトに当たって跳ね返らせることができるのでしょうか?
縦の跳ね返りを考える
まずは画面を縦に移動するスプライトが跳ね返る動作を考えてみましょう。
例としてブロック崩しがわかりやすいでしょう。
ボールが縦方向に移動し、画面下のパドルがボールを跳ね返らせて画面上にあるブロックを消していくゲームです。

ボールがパドルに当たったら跳ね返るようにするには、「(180 – ボールの向き)度に向ける」とすれば跳ね返ります。

例えば、ボールが135度の向きでパドルに当たったら、45度に向いて移動します。
ブロックも同じく画面下からボールが来て、ブロックに当たったときに45度の向きで当たると、次にボールは135度に向いて移動します。
これで縦方向に移動するスプライトは「(180 – 向き)度に向ける」という法則で跳ね返りが可能となることがわかります。
少し余談となりますが、ブロック崩しはパドルに当たって跳ね返るボールが一定方向より、少し変化したほうが面白いので「(ボールのX座標 – パドルのX座標)x 2 度に向ける」といったようなことをします。
こうした場合、パドルの左側に当たった場合と右側に当たった場合で跳ね返る角度を変えることができます。

パドルが画面左右中央のX座標が0の場所にあるとして、ボールのX座標が10のところで当たった場合は、20度に向いて跳ね返ります。(パドル右側)
ボールのX座標が-10のところで当たった場合は、-20度に向いて跳ね返ります。(パドル左側)
横の跳ね返りを考える
今度は横の跳ね返りを考えます。
垂直のパドルを画面左右に配置してボールを交互に打ち返すゲームを想像してみましょう。
この場合はボールが横方向に移動し、パドルがボールを跳ね返らせてボールを反対方向へ移動させます。

先程の縦の跳ね返りの計算で向きを変えようとしても思ったようには動きません。
横方向に移動するのを跳ね返るようにするには、「(-1 x ボールの向き)度に向ける」とすれば跳ね返ります。
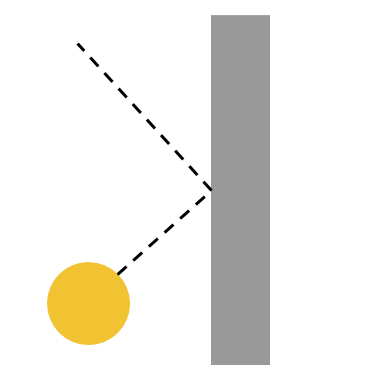
例えば、ボールが45度の向きでパドルに当たったら、-45度に向いて移動します。
Scratchの横方向は右側が0~180度、左側が-179~-1度となり、向いている方向がプラス度のときは右でマイナス度のときは左になります。
なので、向いている方向のプラスとマイナスを反転させれば跳ね返る動作をします。
斜めの跳ね返りを考える
これまでは、横か縦に向いているスプライトに当たったときの跳ね返りを考えました。
もしスプライトが斜めに向いているとどのようになるのでしょうか?
これに縦か横の跳ね返りの法則で向きを変えると変な動作に見えるでしょう。

期待するのは斜めに向いたパドルに当たったときもこの図のように跳ね返ることです。
斜めに向いているパドルに当たって跳ね返るようにするには、ボールを「((パドルの向き + 90)x 2 – ボールの向き)度に向ける」とすれば跳ね返ります。
例えば、45度に向いているパドルに90度で移動してきたボールが当たれば、180度に向いて移動します。
この方法を使えば衝突されるスプライトと衝突するスプライトの向きによって、跳ね返る角度を算出するのでどの向きにスプライトがいても跳ね返ることができます。
なので、縦でも横でも斜めでも全ての方向で使えて便利です。
そしてこれは、衝突するスプライトの向きがわかるものだけに適用できます。
つまりパドルのような直線の壁に当たるプログラムには便利な法則となります。
※注意点
衝突するスプライトの向きによって跳ね返る角度を決めるので、そのスプライトの向きと違うところに当たるとスプライトに沿った動きとなります。
例えば、正方形のスプライトを壁としたとき、これが90度に向いて画面にあるとします。
左右のどちらかスプライトの横に当たれば、期待通りに跳ね返りますが、上下の辺に当たった場合はスプライトの中を抜けるような動きになります。
なので、パドルや壁を作るときはできるだけ薄く、角に当たるとスプライトに沿って動くことを考慮して作るといいでしょう。
まとめ
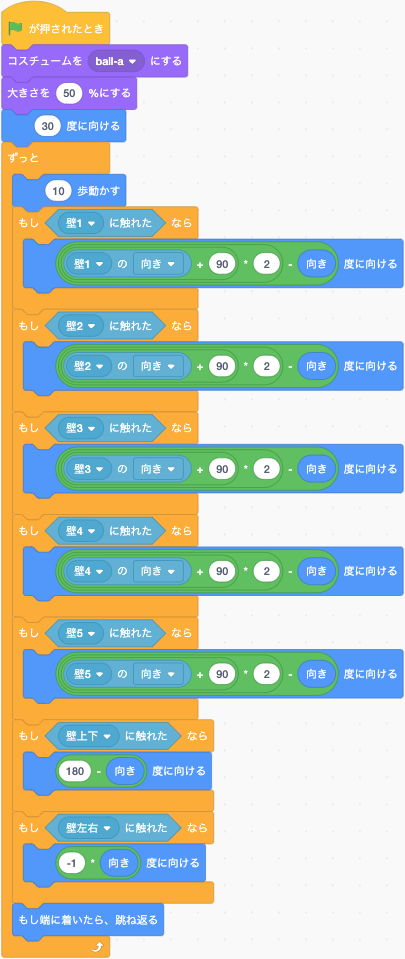
以下はボールのコードをまとめたものです。