• データ・変数
• 図形の描画
• 色の指定
• 点と直線の描画
• 円と円弧の描画
• 四角形と三角形の描画
• 多角形の描画
• 曲線の描画
• 繰り返し
• 条件分岐
• 関数
• アニメーション
• イベント動作
• 画像
• 配列
• オブジェクト指向プログラミング
• 数理造形
• やってみよう

不思議なことに自然界の様々な生物は一定の法則で形作られているものが多くあります。

また、地球や月のように一定の法則で動作しているものも多くあります。

そのような法則を使うとさらに表現が豊かなものを作ることができます。

ここではそういった算術でよく用いられる三角関数を使用して表現する例を取り上げます。

三角関数は高校時代に習ったはずの、サイン、コサイン、タンジェントや直角三角形の各辺の長さの法則などです。

ここでは学術的な詳細は説明しませんが、これらを使うとこんなことができるという説明をします。

円周上の座標

三角関数を使えば円周上の座標を特定することができます。

コサイン(余弦)は円周上のx座標を求めます。サイン(正弦)は円周上のy座標を求めます。

半径1の円の中心から円周上までの角度をシータ(θ)としたとき、「cos(θ) = x座標」「sin(θ) = y座標」となります。

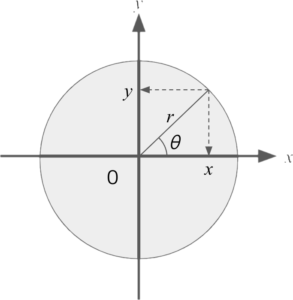
例えば、半径10の円周上の座標は「10 * cos(θ) = x座標」「10 * sin(θ) = y座標」となります。

半径をrとすると円周上の座標は「r * cos(θ) = x座標」「r * sin(θ) = y座標」となります。

このとき、角度であるシータ(θ)はラジアンを使います。

ラジアンはもう1つの角度を表す単位です。通常、円一周の角度を表すときは0°から360°で表します。

これをラジアンに置き換えると、円一周は0から約6.28となります。

ラジアンは弧度法といって、円周上でその円の半径と同じ長さの弧を切り取る2本の半径が作る角度が1ラジアンです。

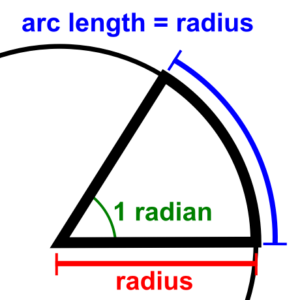
そのため180°は約3.14となります。つまりパイ(π)です。なので、360°は2πで約6.28となります。

ということは1°は「約3.14/180 = π/180」となります。

角度は円の右が0°でそこから時計回りに増えていきます。

この計算式を使えば円周上の座標位置に図形を描画し、少しずつ動かすことで太陽を周回する惑星を表現したり、アナログ時計などのようなものも表現できるようになります。

float p=0;
float radius=200;
void setup() {
  size(500,500);
}

void draw() {
  background(0);
  noStroke();
  fill(255,150,0);
  ellipse(width/2,height/2,40,40);
  float x = width/2 + radius * cos(p*PI/180);
  float y = height/2 + radius * sin(p*PI/180);
  fill(0,200,200);
  ellipse(x,y,20,20);
  float mx = x + 30 * cos(p*12*PI/180);
  float my = y + 30 * sin(p*12*PI/180);
  fill(255);
  ellipse(mx,my,5,5);
  p+=0.1;
}

このコードは太陽を周回する地球を表現しています。地球を周回する月も表現しています。

1行目のp変数は角度(度数法の値)を格納します。初期値0です。

2行目のradius変数は画面中央からの半径を格納しています。

11行目で画面中央に太陽となる円を描画しています。

12〜13行目で画面中央からradius変数の値だけの半径の円周上の座標を求めています。

p変数を使って少しずつ(0.1ずつ)角度を変えています。

15行目でこの座標を使って地球となる円を描画しています。

16〜17行目で月となる円の座標を求めています。

x,y変数には地球の座標が入っているので、そこを中心として半径30の円周上の座標を求めています。

月は地球が太陽の周りを一周するときに月は地球の周りを12回まわるので12をかけています。

19行目でその座標を使って月となる円を描画しています。

20行目で角度の変化量のp変数の値を0.1ずつ変えています。

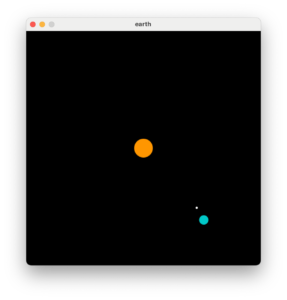
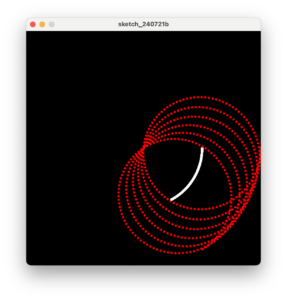
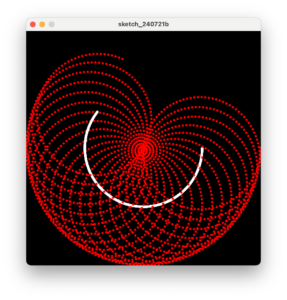
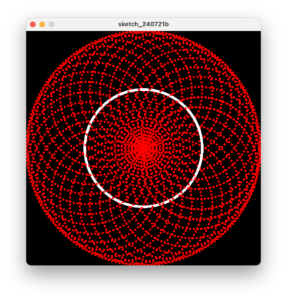
このコードを少し修正し次の模様を描くようにします。

float p=0;
float radius=200;
void setup() {
  size(500,500);
  background(0);
  noStroke();
  radius = width/4;
}

void draw() {
  float x = width/2 + radius * cos(p*PI/180);
  float y = height/2 + radius * sin(p*PI/180);
  fill(255);
  ellipse(x,y,5,5);
  float mx = x + radius * cos(p*36*PI/180);
  float my = y + radius * sin(p*36*PI/180);
  fill(255,0,0);
  ellipse(mx,my,5,5);
  p+=0.1;
}

7行目でradius変数の値を画面幅の4/1にします。

11〜14行目は太陽を表現した円を削除し、地球を表現した円は白の小さな円に変えます。

15〜18行目で月を表現した円をradius変数を半径とした円周上に変え、角度の変化量も3倍にします。

Processingでは度数法の角度(0~360)を使ってラジアンに変換するradians()関数が用意されています。

radians()を使えば45や127といった角度の値でcos()やsin()などを使うことができます。

つまり「radians(1) = π/180」「radians(180) = π」となるわけです。

上記コードの座標を算出している箇所は次のように記述することもできます。

  float x = width/2 + radius * cos(radians(p));
  float y = height/2 + radius * sin(radians(p));

  float mx = x + radius * cos(radians(p*36));
  float my = y + radius * sin(radians(p*36));

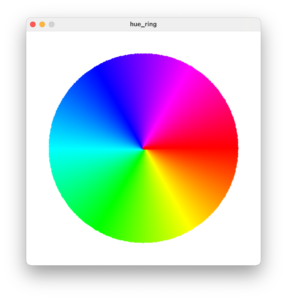
その他の例として、画面中央の座標を中心に円周上の座標間の線を描き、色相環を描画してみましょう。

void setup() {
  size(500,500);
  colorMode(HSB,360,100,100);
}

void draw() {
  float radius = 200;
  background(0,0,255);
  for (int i=0; i<360; i++) {
    float x = width/2 + radius * cos(radians(i));
    float y = height/2 + radius * sin(radians(i));
    strokeWeight(5);
    stroke(i,100,100);
    line(width/2,height/2,x,y);
  }
}

7行目でカラーモードをHSBに変更します。

10〜17行目で360本の線を画面中央を軸に1周描画しています。

そのときの線の色の色相を0〜359まで変化させながら描いています。

正多角形とn芒星の描画

さらに他の例として、円周上の座標を等間隔に配置し正多角形を描画してみましょう。

int point = 5;
void setup() {
  size(500,500);
}

void draw() {
  background(255);
  fill(255,0,0);
  polygon(width/2,height/2,100,point);
}

void polygon(float x,float y,float radius,int points) {
  beginShape();
  for (int i=0; i<points; i++) {
    float px = x + radius * cos(i * TWO_PI/points);
    float py = y + radius * sin(i * TWO_PI/points);
    vertex(px,py);
  }
  endShape(CLOSE);
}

void keyPressed() {
  if (keyCode >= 49 && keyCode <= 57) {
    point = keyCode-48;
  }
}

12〜20行目で正多角形を描画するコードを関数polygonにまとめています。

引数に中心となる座標、半径、頂点の数を受け入れるようにしています。

この関数は指定された中心座標から指定された半径の円周上に、指定された頂点の数を均等に割り当てた座標で多角形を描画しています。

頂点の数はグローバル変数pointに格納し、初期値は5としています。

22〜26行目で数字キーが押されたときだけ、その数をpoint変数に格納し、描画がその数の正多角形となります。

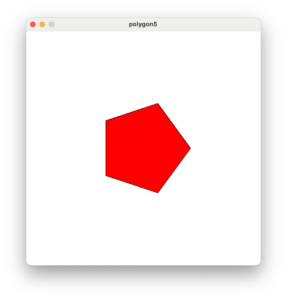
プログラム起動時は五角形が表示されます。そしてキーボードの8を押すと八角形が表示されます。

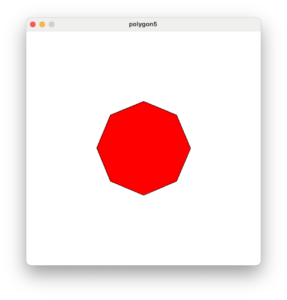
このコードを改造し、n芒星を描画してみます。

int point = 5;
void setup() {
  size(500,500);
}

void draw() {
  background(255);
  fill(255,255,0);
  star(width/2,height/2,100,40,point);
}

void star(float x,float y,float radius1,float radius2,int n) {
    float angle = TWO_PI/(n*2);
    beginShape();
    for (int i=0; i<n*2; i++) {
      float radius = 0;
      if (i % 2 == 0) {
        radius = radius1;
      } else {
        radius = radius2;
      }
      float sx = x+radius*cos(i * angle);
      float sy = y+radius*sin(i * angle);
      vertex(sx,sy);
    }
    endShape(CLOSE);
}

void keyPressed() {
  if (keyCode >= 49 && keyCode <= 57) {
    point = keyCode-48;
  }
}

2つの大きさが異なる円の円周上にそれぞれ交互に座標を配置することで、星型を描画することができます。

12行目でstar関数に書き直し、引数に2つの円の半径を受け入れるようにします。

頂点と頂点の間に小さな円の円周上の座標を配置することで星の形となります。

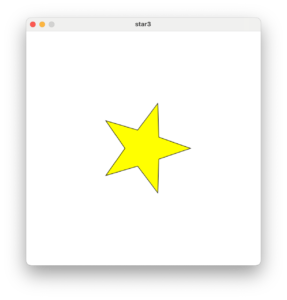
プログラム起動時は五芒星が表示されます。そしてキーボードの7を押すと七芒星が表示されます。